Perform chi-square test of independence or Fisher's exact test (automatically selected based on expected frequencies) with publication-ready visualization. Designed for analyzing the association between two categorical variables.
Arguments
- data
A data frame containing the variables.
- var1
Column name for the first categorical variable (row variable). Supports both quoted and unquoted names via NSE.
- var2
Column name for the second categorical variable (column variable). Supports both quoted and unquoted names via NSE.
- method
Character. Test method: "auto" (default), "chisq", "fisher", or "mcnemar". When "auto", the function intelligently selects based on expected frequencies and table size. WARNING: "mcnemar" is ONLY for paired/matched data (e.g., before-after measurements on the same subjects). It tests marginal homogeneity, NOT independence. Do NOT use McNemar's test for independent samples - use "chisq" or "fisher" instead.
- correct
Logical or
NULL. Apply Yates' continuity correction? IfNULL(default), automatically applied for 2x2 tables with expected frequencies < 10.- conf.level
Numeric. Confidence level for the interval. Default is 0.95.
- plot_type
Character. Type of plot: "mosaic" (default), "bar_grouped", "bar_stacked", or "heatmap".
- show_p_value
Logical. Display p-value on the plot? Default is
TRUE.- p_label
Character. P-value label format: "p.format" (numeric p-value, default) or "p.signif" (stars).
- palette
Character. Color palette name from evanverse palettes. Default is "qual_vivid". Set to
NULLto use ggplot2 defaults.- verbose
Logical. Print diagnostic messages? Default is
TRUE.- ...
Additional arguments (currently unused, reserved for future extensions).
Value
An object of class quick_chisq_result containing:
- plot
A ggplot object with the association visualization
- test_result
The htest object from
chisq.test()orfisher.test()- method_used
Character string of the test method used
- contingency_table
The contingency table (counts)
- expected_freq
Matrix of expected frequencies
- pearson_residuals
Pearson residuals for each cell
- effect_size
Cramer's V effect size measure
- descriptive_stats
Data frame with frequencies and proportions
- auto_decision
Details about automatic method selection
- timestamp
POSIXct timestamp of analysis
Details
"Quick" means easy to use, not simplified or inaccurate.
This function performs full statistical testing with proper assumption checking:
Automatic Method Selection (method = "auto")
The function uses an intelligent algorithm based on expected frequencies:
All expected frequencies >= 5: Standard chi-square test
2x2 table with any expected frequency < 5: Fisher's exact test
Larger table with expected frequency < 5: Chi-square with warning
2x2 table with 5 <= expected frequency < 10: Chi-square with Yates' correction
Effect Size
Cramer's V is calculated as a measure of effect size:
Small effect: V = 0.1
Medium effect: V = 0.3
Large effect: V = 0.5
Important Notes
Categorical variables: Both variables must be categorical or will be coerced to factors.
Sample size: Fisher's exact test may be computationally intensive for large tables.
Missing values: Automatically removed with a warning.
Low frequencies: Cells with expected frequency < 5 may lead to unreliable results.
Examples
# Example 1: Basic usage with automatic method selection
set.seed(123)
data <- data.frame(
treatment = sample(c("A", "B", "C"), 100, replace = TRUE),
response = sample(c("Success", "Failure"), 100, replace = TRUE,
prob = c(0.6, 0.4))
)
result <- quick_chisq(data, var1 = treatment, var2 = response)
#> ℹ treatment converted to factor with 3 levels.
#> ℹ response converted to factor with 2 levels.
#> ! Failed to load palette 'qual_vivid': Palette "qual_vivid" not found under "sequential", but exists under "qualitative". Try: `get_palette("qual_vivid", type = "qualitative")`. Using default colors.
#> ! ggmosaic package not available. Using grouped bar chart instead.
print(result)
#>
#> ===========================================================
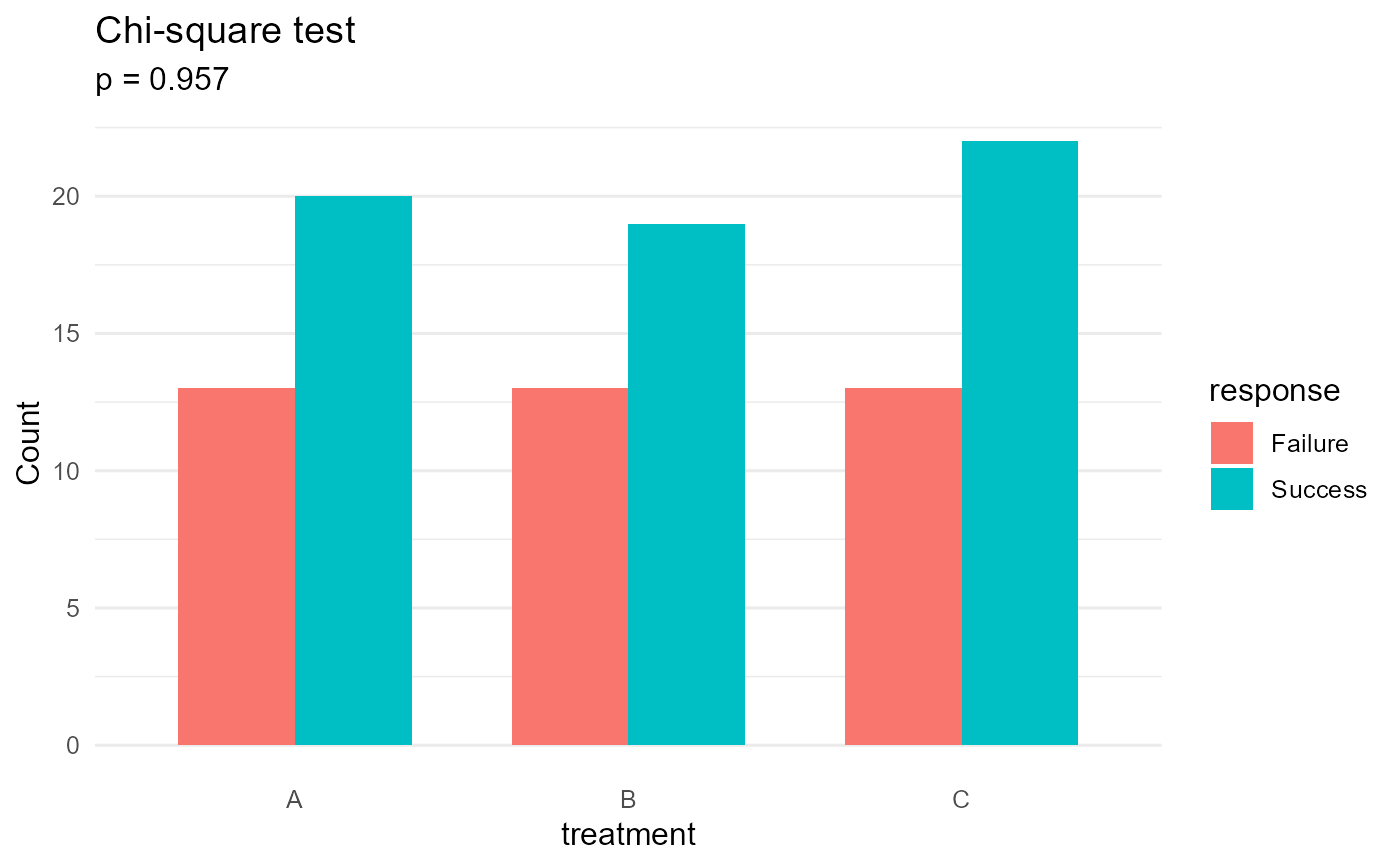#> Quick Chi-Square Test Result
#> ===========================================================
#>
#> Method: Chi-square test
#> Test statistic: 0.088
#> Degrees of freedom: 2
#> P-value: 0.9568
#>
#> Effect Size (Cramer's V): 0.03 ( negligible )
#>
#> Contingency Table:
#>
#> Failure Success
#> A 13 20
#> B 13 19
#> C 13 22
#>
#> Decision: All expected frequencies adequate: using standard chi-square test
#>
#> Timestamp: 2025-11-12 17:36:55
#> ===========================================================
# Example 2: 2x2 table
data_2x2 <- data.frame(
gender = rep(c("Male", "Female"), each = 50),
disease = sample(c("Yes", "No"), 100, replace = TRUE)
)
result <- quick_chisq(data_2x2, var1 = gender, var2 = disease)
#> ℹ gender converted to factor with 2 levels.
#> ℹ disease converted to factor with 2 levels.
#> ! Failed to load palette 'qual_vivid': Palette "qual_vivid" not found under "sequential", but exists under "qualitative". Try: `get_palette("qual_vivid", type = "qualitative")`. Using default colors.
#> ! ggmosaic package not available. Using grouped bar chart instead.
# Example 3: Customize visualization
result <- quick_chisq(data,
var1 = treatment,
var2 = response,
plot_type = "bar_grouped",
palette = "qual_balanced")
#> ℹ treatment converted to factor with 3 levels.
#> ℹ response converted to factor with 2 levels.
#> ! Failed to load palette 'qual_balanced': Palette "qual_balanced" not found under "sequential", but exists under "qualitative". Try: `get_palette("qual_balanced", type = "qualitative")`. Using default colors.
# Example 4: Manual method selection
result <- quick_chisq(data,
var1 = treatment,
var2 = response,
method = "chisq",
correct = FALSE)
#> ℹ treatment converted to factor with 3 levels.
#> ℹ response converted to factor with 2 levels.
#> ! Failed to load palette 'qual_vivid': Palette "qual_vivid" not found under "sequential", but exists under "qualitative". Try: `get_palette("qual_vivid", type = "qualitative")`. Using default colors.
#> ! ggmosaic package not available. Using grouped bar chart instead.
# Access components
result$plot # ggplot object
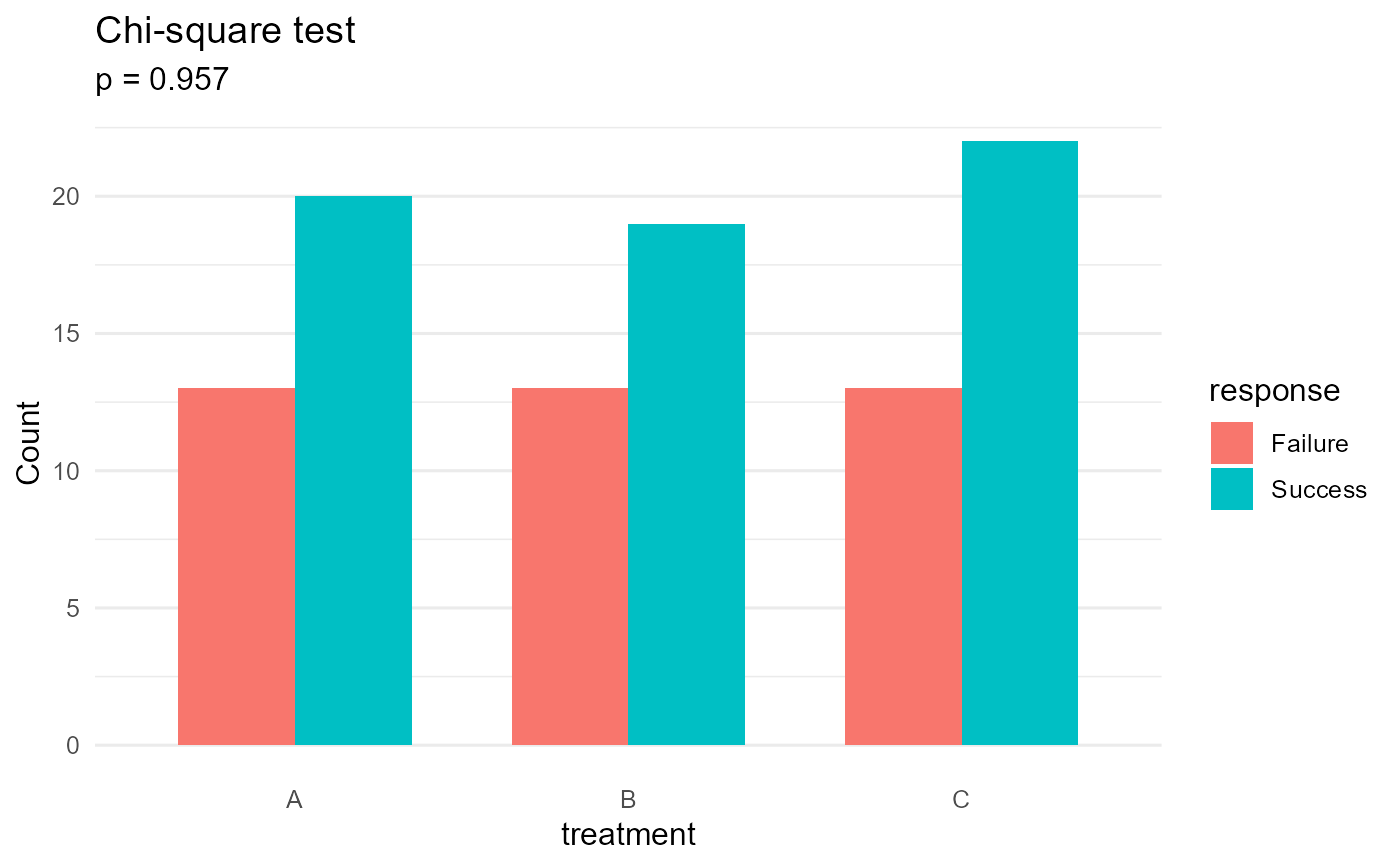result$test_result # htest object
#>
#> Pearson's Chi-squared test
#>
#> data: cont_table
#> X-squared = 0.088413, df = 2, p-value = 0.9568
#>
result$contingency_table # Contingency table
#>
#> Failure Success
#> A 13 20
#> B 13 19
#> C 13 22
result$pearson_residuals # Pearson residuals
#>
#> Failure Success
#> A 0.03623715 -0.02897487
#> B 0.14719601 -0.11769647
#> C -0.17593289 0.14067419
summary(result) # Detailed summary
#> ===========================================================
#> Quick Chi-Square Test - Detailed Summary
#> ===========================================================
#>
#> Method: Chi-square test
#> Timestamp: 2025-11-12 17:36:55
#>
#> -----------------------------------------------------------
#> Test Results:
#> -----------------------------------------------------------
#>
#> Pearson's Chi-squared test
#>
#> data: cont_table
#> X-squared = 0.088413, df = 2, p-value = 0.9568
#>
#>
#> -----------------------------------------------------------
#> Effect Size:
#> -----------------------------------------------------------
#> Cramer's V: 0.03
#> Interpretation: negligible
#>
#> -----------------------------------------------------------
#> Observed Frequencies:
#> -----------------------------------------------------------
#>
#> Failure Success
#> A 13 20
#> B 13 19
#> C 13 22
#>
#> -----------------------------------------------------------
#> Expected Frequencies:
#> -----------------------------------------------------------
#> Failure Success
#> A 12.87 20.13
#> B 12.48 19.52
#> C 13.65 21.35
#>
#> -----------------------------------------------------------
#> Pearson Residuals:
#> -----------------------------------------------------------
#>
#> Failure Success
#> A 0.04 -0.03
#> B 0.15 -0.12
#> C -0.18 0.14
#>
#> Note: Values > |2| indicate significant deviation from independence
#>
#> -----------------------------------------------------------
#> Descriptive Statistics:
#> -----------------------------------------------------------
#> treatment response Count Proportion Percent
#> 1 A Failure 13 0.13 13
#> 2 B Failure 13 0.13 13
#> 3 C Failure 13 0.13 13
#> 4 A Success 20 0.20 20
#> 5 B Success 19 0.19 19
#> 6 C Success 22 0.22 22
#>
#> -----------------------------------------------------------
#> Method Selection Details:
#> -----------------------------------------------------------
#> Table size: 3x2
#> Total N: 100
#> Minimum expected frequency: 12.48
#> Cells with expected freq < 5: 0
#> Proportion of cells < 5: 0
#> Reason: User-specified method: chisq
#>
#> ===========================================================